Na początku dowiesz się, jak przyrównać funkcję do zera i rozwiązać równanie kwadratowe. Następnie omówimy, jak współczynnik kierunkowy wpływa na kształt paraboli oraz jak znaleźć jej wierzchołek. Dzięki tym informacjom, będziesz mógł stworzyć wykres, który nie tylko będzie poprawny, ale także estetyczny.
Kluczowe informacje:- Obliczenie miejsc zerowych funkcji kwadratowej jest pierwszym krokiem w rysowaniu wykresu.
- Współczynnik kierunkowy 'a' decyduje, czy ramiona paraboli są skierowane w górę, czy w dół.
- Wierzchołek paraboli można obliczyć za pomocą wzorów, co ułatwia rysowanie wykresu.
- Tworzenie tabeli wartości dla różnych x zwiększa dokładność wykresu.
- Unikanie typowych błędów, takich jak błędne obliczenia miejsc zerowych, jest kluczowe dla poprawności wykresu.
- Wykresy funkcji kwadratowych mają zastosowanie w różnych dziedzinach, od matematyki po fizykę.
Jak obliczyć miejsca zerowe funkcji kwadratowej dla wykresu
Aby narysować wykres funkcji kwadratowej, kluczowym krokiem jest obliczenie miejsc zerowych tej funkcji. Miejsca zerowe to punkty, w których funkcja przyjmuje wartość zero. Aby je znaleźć, należy przyrównać funkcję do zera i rozwiązać odpowiednie równanie kwadratowe. W praktyce oznacza to, że jeśli mamy funkcję w postaci ogólnej, na przykład y = ax^2 + bx + c, musimy ustawić równanie tak, aby wyglądało jak ax^2 + bx + c = 0.
Po ustawieniu równania na zero, można przejść do jego rozwiązania. W tym celu można skorzystać z wzoru kwadratowego, który jest bardzo przydatny w takich sytuacjach. Wzór ten ma postać x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}. Dzięki niemu możemy szybko obliczyć wartości x, które są miejscami zerowymi funkcji kwadratowej. Przykładowo, dla funkcji y = 2x^2 - 4x - 6, po zastosowaniu wzoru kwadratowego, otrzymamy konkretne wartości miejsc zerowych.Przyrównanie funkcji do zera i rozwiązanie równania
Przyrównanie funkcji kwadratowej do zera to pierwszy krok w procesie obliczania miejsc zerowych. W zależności od współczynników funkcji, mogą wystąpić różne typy równań. Na przykład, jeśli współczynnik a jest równy zero, równanie przestaje być kwadratowe i staje się liniowe. W przeciwnym razie, gdy a jest różne od zera, mamy do czynienia z równaniem kwadratowym, które można rozwiązać za pomocą wzorów kwadratowych lub faktoryzacji.
Wykorzystanie wzorów kwadratowych do obliczeń
Wzór kwadratowy to narzędzie, które pozwala na szybkie obliczenie miejsc zerowych funkcji kwadratowej. Kiedy mamy równanie w postaci ax^2 + bx + c = 0, możemy zastosować wzór x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, aby znaleźć wartości x. Na przykład, dla równania 3x^2 - 6x + 3 = 0, podstawiając do wzoru, obliczamy miejsca zerowe, które wynoszą x = 1.
| Równanie | Miejsca zerowe |
| 2x^2 - 4x - 6 = 0 | x = 3, x = -1 |
| 3x^2 + 6x + 3 = 0 | x = -1 |
| x^2 - 5x + 6 = 0 | x = 2, x = 3 |
Jak określić kształt paraboli i jej ramiona
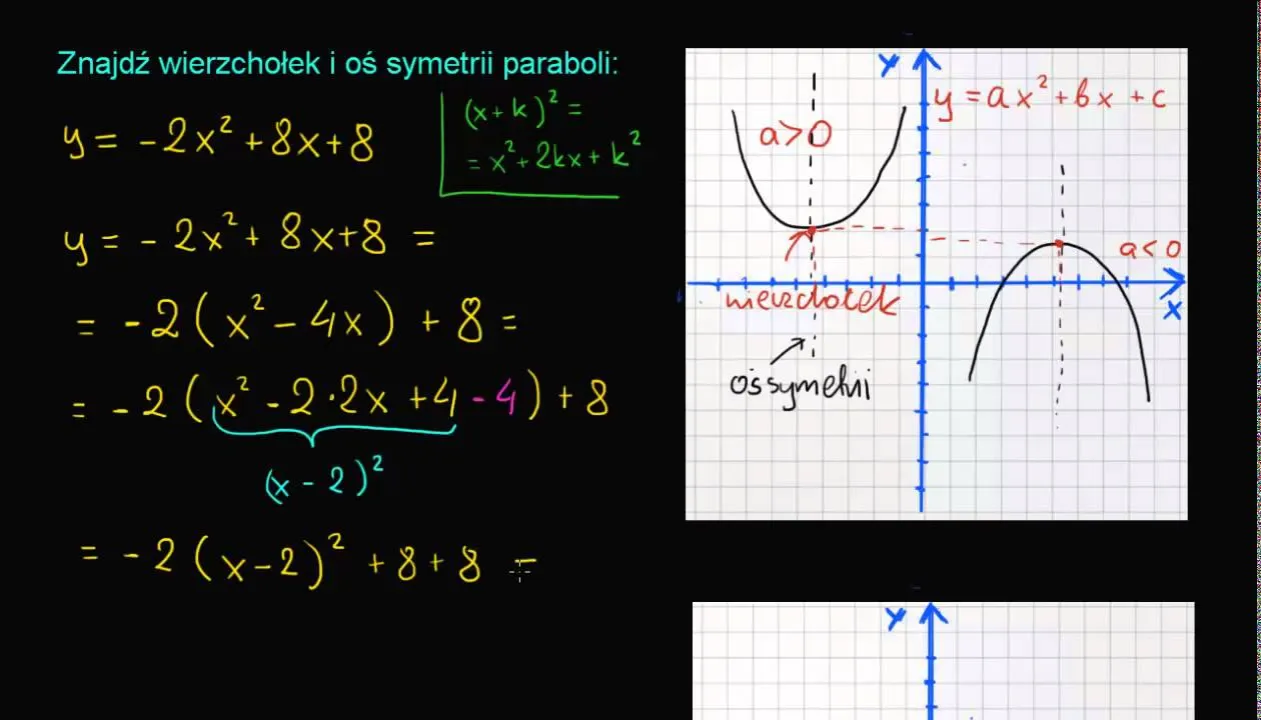
Aby zrozumieć, jak narysować wykres funkcji kwadratowej, musimy najpierw określić kształt paraboli. Kluczowym czynnikiem wpływającym na kierunek ramion paraboli jest współczynnik 'a' w równaniu kwadratowym. Jeśli a jest dodatnie, ramiona paraboli będą skierowane w górę, co oznacza, że funkcja ma minimum. Natomiast jeśli a jest ujemne, ramiona będą skierowane w dół, co wskazuje na maksimum funkcji.
Wartość współczynnika 'a' nie tylko decyduje o kierunku ramion, ale także wpływa na kształt paraboli. Im większa wartość bezwzględna współczynnika a, tym bardziej stroma będzie parabola. Na przykład, dla funkcji y = 2x^2 parabola będzie bardziej stroma w porównaniu do funkcji y = 0.5x^2, która będzie bardziej płaska. To zrozumienie jest kluczowe dla dalszego rysowania wykresu.
Zrozumienie roli współczynnika kierunkowego a w funkcji
Współczynnik 'a' w funkcji kwadratowej ma kluczowe znaczenie dla określenia kształtu i kierunku paraboli. Jeśli a jest równe zero, funkcja przestaje być kwadratowa i staje się liniowa. W przypadku wartości dodatnich a > 0, ramiona paraboli otwierają się w górę, co oznacza, że funkcja osiąga minimum. Z kolei dla wartości ujemnych a < 0, ramiona otwierają się w dół, co wskazuje na maksimum funkcji. To zrozumienie jest fundamentem do dalszej analizy i rysowania wykresów funkcji kwadratowych.
Jak rozpoznać, czy parabola jest skierowana w górę czy w dół
Rozpoznanie kierunku ramion paraboli jest kluczowe dla zrozumienia jej kształtu. Aby to zrobić, wystarczy spojrzeć na wartość współczynnika 'a'. Jeśli a jest dodatnie, ramiona paraboli są skierowane w górę, co oznacza, że funkcja ma minimum. Jeśli natomiast a jest ujemne, ramiona są skierowane w dół, co wskazuje na maksimum funkcji. Zrozumienie tego aspektu jest niezbędne do prawidłowego rysowania wykresu funkcji kwadratowej.
Czytaj więcej: Jak narysować Sanah: krok po kroku, uchwyć jej wyjątkowy styl
Jak znaleźć wierzchołek paraboli dla dokładnego rysunku
Obliczenie wierzchołka paraboli jest kluczowe dla uzyskania dokładnego wykresu funkcji kwadratowej. Wierzchołek, oznaczany jako W(p, q), można obliczyć za pomocą wzorów, które zależą od formy równania kwadratowego. Dla funkcji w postaci ogólnej y = ax^2 + bx + c, współrzędne wierzchołka można obliczyć według wzorów: p = \frac{-b}{2a} oraz q = \frac{-Δ}{4a}, gdzie Δ = b^2 - 4ac. Te formuły pozwalają na szybkie określenie punktu, w którym funkcja osiąga swoje maksimum lub minimum.
Na przykład, dla funkcji y = 2x^2 - 8x + 6, możemy obliczyć współrzędne wierzchołka. Najpierw obliczamy p: p = \frac{-(-8)}{2 \cdot 2} = 2. Następnie obliczamy Δ: Δ = (-8)^2 - 4 \cdot 2 \cdot 6 = 64 - 48 = 16. Teraz możemy znaleźć q: q = \frac{-16}{4 \cdot 2} = -2. W rezultacie wierzchołek paraboli znajduje się w punkcie W(2, -2).
Wzory do obliczania współrzędnych wierzchołka W(p, q)
Aby znaleźć współrzędne wierzchołka W(p, q) paraboli, należy skorzystać z kilku prostych wzorów. Dla funkcji w postaci ogólnej y = ax^2 + bx + c, współrzędne wierzchołka można obliczyć przy użyciu wzoru: p = \frac{-b}{2a}. Z kolei q można znaleźć, podstawiając wartość p do oryginalnej funkcji: q = a(p)^2 + b(p) + c. Dla funkcji w postaci kanonicznej y = a(x - p)^2 + q, współrzędne wierzchołka są już bezpośrednio podane jako W(p, q).
Jak wykorzystać postać kanoniczną funkcji do rysunku
Postać kanoniczna funkcji kwadratowej jest niezwykle przydatna, gdy chcemy szybko zidentyfikować wierzchołek paraboli. Używając postaci y = a(x - p)^2 + q, możemy bezpośrednio odczytać współrzędne wierzchołka jako W(p, q). To upraszcza proces rysowania wykresu, ponieważ nie musimy obliczać wierzchołka z równania ogólnego. Na przykład, w funkcji y = 3(x - 1)^2 + 2, wierzchołek znajduje się w punkcie W(1, 2), co ułatwia dalsze rysowanie wykresu.
Jak narysować wykres funkcji kwadratowej krok po kroku
Aby narysować wykres funkcji kwadratowej, warto podejść do tego zadania krok po kroku. Pierwszym krokiem jest obliczenie miejsc zerowych funkcji oraz wierzchołka paraboli. Następnie należy określić kilka punktów, które pomogą w dokładnym odwzorowaniu kształtu wykresu. Kluczowe jest, aby upewnić się, że wszystkie obliczenia są poprawne, ponieważ to wpłynie na ostateczny wygląd wykresu.
Po obliczeniu miejsc zerowych oraz wierzchołka, warto stworzyć tabelę wartości. Dzięki temu można łatwo zobaczyć, jak zmienia się wartość funkcji w zależności od wybranych wartości x. Warto również pamiętać o symetrii paraboli względem osi Y, co może ułatwić rysowanie wykresu. Im więcej punktów wyznaczymy, tym dokładniejszy będzie nasz wykres.
Sporządzanie tabeli wartości dla różnych x dla dokładności
Tworzenie tabeli wartości to kluczowy krok w procesie rysowania wykresu funkcji kwadratowej. Aby to zrobić, należy wybrać kilka wartości x, które są istotne dla funkcji. Następnie, dla każdej z tych wartości, obliczamy odpowiadające im wartości y za pomocą równania funkcji. Na przykład, dla funkcji y = x^2 - 4x + 3, możemy wybrać wartości x = 0, 1, 2, 3, 4 i obliczyć odpowiadające wartości y.
Jak zapewnić symetrię wykresu względem osi Y
Symetria parabol jest istotnym aspektem, który należy uwzględnić podczas rysowania wykresu. Parabola jest symetryczna względem prostej przechodzącej przez jej wierzchołek i równoległej do osi Y. Oznacza to, że jeśli znamy jeden punkt na wykresie, możemy łatwo znaleźć odpowiadający mu punkt po drugiej stronie wierzchołka. W praktyce, jeśli mamy punkt (x, y), to jego symetryczny odpowiednik będzie miał współrzędne (2p - x, y), gdzie p to współrzędna x wierzchołka.
Jak unikać typowych błędów przy rysowaniu parabol
Rysowanie wykresu funkcji kwadratowej może być wyzwaniem, a popełnianie błędów jest powszechne, szczególnie dla początkujących. Warto znać najczęstsze pomyłki, aby móc ich unikać. Do typowych błędów należy niepoprawne obliczenie miejsc zerowych, co może prowadzić do błędnych punktów na wykresie. Inną powszechną pomyłką jest niewłaściwe określenie kierunku ramion paraboli, co wpływa na ogólny kształt wykresu.
Ważne jest również, aby dokładnie obliczyć współrzędne wierzchołka, ponieważ ich błędne wartości mogą całkowicie zniekształcić wykres. Ponadto, niektórzy mogą zapomnieć o symetrii paraboli, co prowadzi do nierównomiernego rysowania. Aby uniknąć tych problemów, warto regularnie sprawdzać swoje obliczenia oraz stosować się do ustalonych kroków podczas rysowania wykresu.
Najczęstsze pomyłki przy obliczeniach miejsc zerowych
Podczas obliczania miejsc zerowych funkcji kwadratowej, wiele osób popełnia typowe błędy. Często zdarza się, że niepoprawnie stosują wzór kwadratowy, co prowadzi do błędnych wyników. Inne powszechne pomyłki to błędne obliczenia wartości współczynników a, b i c, które są kluczowe dla zastosowania wzoru. Dodatkowo, nieuwzględnienie wartości Δ (delta) w obliczeniach może skutkować pominięciem ważnych informacji o liczbie miejsc zerowych.
Jak poprawnie interpretować wyniki obliczeń dla wykresu
Poprawna interpretacja wyników obliczeń jest kluczowa dla rysowania wykresu funkcji kwadratowej. Miejsca zerowe powinny być dokładnie zaznaczone na wykresie, a ich wartości muszą być zgodne z obliczeniami. Warto również pamiętać, że wierzchołek paraboli, obliczony na podstawie wartości p i q, powinien być umiejscowiony w odpowiednim punkcie, co wpłynie na kształt wykresu. Zrozumienie, jak te elementy wpływają na wykres, pozwala na stworzenie dokładniejszej i bardziej estetycznej paraboli.
Jak wykorzystać wykresy funkcji kwadratowej w analizie danych
Wykresy funkcji kwadratowej nie tylko służą do wizualizacji równań, ale mogą być również niezwykle przydatne w analizie danych. W wielu dziedzinach, takich jak ekonomia czy inżynieria, funkcje kwadratowe mogą modelować zjawiska, takie jak koszty produkcji czy trajektorie obiektów. Zrozumienie, jak rysować i interpretować te wykresy, pozwala na lepsze prognozowanie trendów oraz podejmowanie bardziej świadomych decyzji.
Na przykład, w analizie statystycznej wykresy funkcji kwadratowej mogą być używane do identyfikacji i analizy zjawisk nieliniowych w zbiorach danych. Dzięki zastosowaniu regresji kwadratowej, można uzyskać model, który lepiej dopasowuje się do danych niż regresja liniowa. To podejście umożliwia odkrywanie ukrytych wzorców i relacji, co jest kluczowe w badaniach naukowych oraz w praktycznych zastosowaniach w biznesie.

