Rysowanie funkcji matematycznych może wydawać się skomplikowane, ale z odpowiednimi narzędziami i metodami, każdy może to zrobić bez stresu i błędów. W tym artykule omówimy różne metody rysowania funkcji, od prostych funkcji liniowych po bardziej złożone funkcje kwadratowe i z wartością bezwzględną. Dzięki krok po kroku instrukcjom oraz wskazówkom, nauczysz się, jak efektywnie tworzyć wykresy, które pomogą zrozumieć matematyczne zależności.
Wybór odpowiednich narzędzi jest kluczowy dla skutecznego rysowania funkcji. Możesz korzystać z programów komputerowych, aplikacji online lub zwykłego papieru milimetrowego. Każda z tych metod ma swoje zalety, a w artykule znajdziesz szczegółowe instrukcje, które pomogą Ci zdecydować, która z nich będzie najlepsza dla Ciebie.Kluczowe informacje:- Rysowanie funkcji wymaga zrozumienia podstawowych zasad matematycznych, takich jak współrzędne i kształt wykresu.
- Do rysowania funkcji można wykorzystać różne narzędzia, zarówno cyfrowe, jak i tradycyjne.
- Każdy typ funkcji, jak liniowe, kwadratowe czy z wartością bezwzględną, wymaga innego podejścia przy rysowaniu.
- Programy do rysowania wykresów umożliwiają łatwe wprowadzanie wzorów i automatyczne generowanie wykresów.
- Znajomość metod rysowania funkcji pozwala na lepsze zrozumienie matematyki i jej zastosowań w praktyce.
Jak narysować funkcje matematyczne krok po kroku dla początkujących
Rysowanie funkcji matematycznych to umiejętność, która może wydawać się trudna, ale z odpowiednim podejściem każdy może ją opanować. Zrozumienie podstawowych zasad rysowania funkcji jest kluczowe dla dalszego rozwoju w matematyce. Wiedza na temat różnych typów funkcji oraz metod ich przedstawiania na wykresie pozwala nie tylko na lepsze zrozumienie matematyki, ale także na zastosowanie tej wiedzy w praktyce, na przykład w analizie danych czy w inżynierii.
Aby skutecznie narysować funkcję, warto znać kilka podstawowych kroków i technik. Kluczowe jest wybranie odpowiednich narzędzi, które ułatwią cały proces. Możesz korzystać z programów komputerowych, aplikacji mobilnych lub tradycyjnych narzędzi, takich jak papier milimetrowy. W dalszej części artykułu omówimy konkretne metody i narzędzia, które pomogą Ci w rysowaniu funkcji.Wybór odpowiednich narzędzi do rysowania funkcji matematycznych
Wybór odpowiednich narzędzi jest kluczowy dla efektywnego rysowania funkcji. Istnieje wiele opcji, które mogą pomóc w tym procesie. Możesz korzystać zarówno z programów komputerowych, jak i z tradycyjnych narzędzi, co daje dużą elastyczność w podejściu do rysowania wykresów.
- GeoGebra - popularne oprogramowanie do nauki matematyki, które umożliwia rysowanie różnych funkcji oraz ich analizę.
- Desmos - intuicyjna aplikacja online, która pozwala na szybkie tworzenie wykresów funkcji matematycznych.
- Graphmatica - program, który umożliwia rysowanie wykresów funkcji oraz ich modyfikację przy użyciu prostego interfejsu.
- Wykresy na papierze milimetrowym - tradycyjna metoda, która pozwala na manualne rysowanie funkcji, idealna do nauki podstaw.
- Microsoft Excel - narzędzie, które umożliwia tworzenie wykresów na podstawie danych, co jest przydatne w analizie statystycznej.
- Python z biblioteką Matplotlib - dla bardziej zaawansowanych użytkowników, pozwala na programowe rysowanie wykresów funkcji.
Podstawowe zasady rysowania funkcji liniowych i kwadratowych
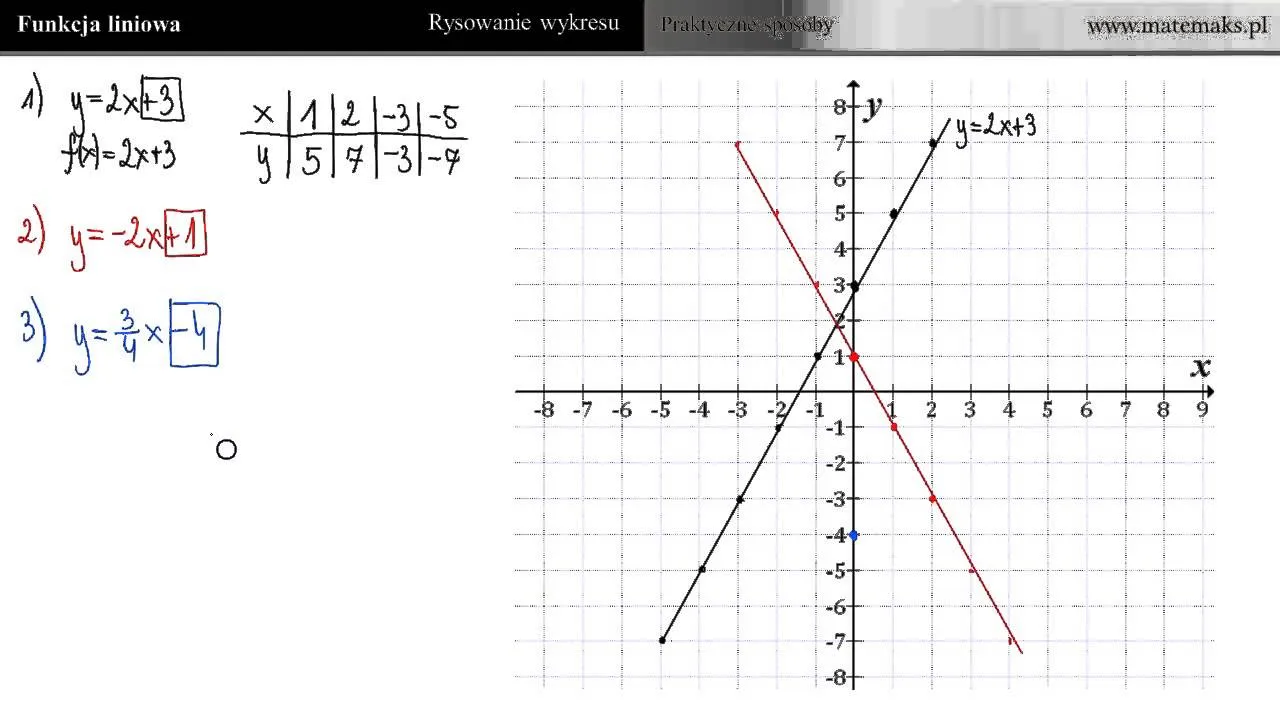
Rysowanie funkcji liniowych i kwadratowych to fundament, na którym opiera się wiele bardziej złożonych koncepcji matematycznych. Funkcje liniowe mają prostą postać, która można opisać równaniem w formie y = mx + b, gdzie m to współczynnik kierunkowy, a b to wyraz wolny. Zrozumienie tych dwóch elementów pozwala na łatwe określenie, jak wygląda wykres funkcji. Na przykład, dla funkcji y = 2x + 3, współczynnik kierunkowy wynosi 2, co oznacza, że dla każdej jednostki wzrostu x, y wzrasta o 2 jednostki, a punkt przecięcia z osią y to 3.Funkcje kwadratowe, z drugiej strony, mają bardziej skomplikowany kształt i są opisane równaniem w postaci y = ax² + bx + c. Kluczowymi elementami są wierzchołek oraz os symetrii. Wierzchołek można obliczyć, korzystając z wzoru x = -b/(2a), a następnie obliczając wartość y dla tej x. Na przykład, dla funkcji y = x² - 4x + 3, wierzchołek znajduje się w punkcie (2, -1), co pozwala na narysowanie parabolii, która otwiera się w górę.
Przykłady funkcji liniowych i kwadratowych
Oto kilka przykładów funkcji liniowych i kwadratowych, które pomogą zobrazować te zasady:
- Funkcja liniowa: y = 3x - 2; współczynnik kierunkowy wynosi 3, a punkt przecięcia z osią y to -2.
- Funkcja kwadratowa: y = -x² + 4x - 3; wierzchołek znajduje się w punkcie (2, 1), a parabola otwiera się w dół.
- Funkcja liniowa: y = -1/2x + 5; współczynnik kierunkowy wynosi -1/2, co oznacza, że linia opada.
- Funkcja kwadratowa: y = 2x² - 8x + 6; wierzchołek można obliczyć, a jego wartość to (2, -2).
Jak narysować funkcje kwadratowe i ich wykresy
Aby narysować funkcje kwadratowe, należy najpierw zrozumieć ich ogólną postać, która jest opisana równaniem y = ax² + bx + c. Kluczowymi krokami w rysowaniu wykresu funkcji kwadratowej są znalezienie wierzchołka oraz osi symetrii. Wierzchołek można obliczyć za pomocą wzoru x = -b/(2a), a następnie podstawiając tę wartość do równania, aby uzyskać współrzędne wierzchołka. Na przykład, dla funkcji y = 2x² - 8x + 6, wierzchołek znajduje się w punkcie (2, -2).
Po ustaleniu wierzchołka i osi symetrii, można narysować parabolę. Ważne jest, aby zaznaczyć kilka punktów na wykresie, aby uzyskać dokładniejszy kształt parabolii. Dla przykładu, jeśli mamy funkcję y = x² - 4, możemy obliczyć wartości y dla różnych wartości x, aby uzyskać punkty, które pomogą w narysowaniu wykresu. W efekcie, wykres funkcji kwadratowej będzie miał charakterystyczny kształt litery U.
| Funkcja kwadratowa | Równanie | Wierzchołek |
|---|---|---|
| Funkcja 1 | y = x² - 2x + 1 | (1, 0) |
| Funkcja 2 | y = -x² + 4x - 3 | (2, 1) |
| Funkcja 3 | y = 2x² - 8x + 6 | (2, -2) |
Rysowanie funkcji z wartością bezwzględną z łatwością
Rysowanie funkcji z wartością bezwzględną jest prostsze, gdy zrozumiesz, jak zmienia się kształt wykresu w zależności od parametrów. Ogólna postać funkcji z wartością bezwzględną to y = a|x - p| + q, gdzie p i q określają przesunięcie wykresu. Wartość bezwzględna tworzy charakterystyczny kształt V, co oznacza, że wykres jest symetryczny względem osi x = p.
Dla przykładu, w funkcji y = |x - 3| + 2, wierzchołek znajduje się w punkcie (3, 2). Aby narysować tę funkcję, warto zaznaczyć punkty po obu stronach wierzchołka, co pozwoli uzyskać pełny obraz wykresu. Rysowanie funkcji z wartością bezwzględną można zrealizować poprzez narysowanie wykresu funkcji liniowej w dwóch częściach, które są odbiciem względem osi poziomej.
Jak wykorzystać programy do rysowania funkcji matematycznych
Wykorzystanie programów do rysowania funkcji matematycznych może znacznie ułatwić proces graficznego przedstawiania różnych funkcji. Dzięki nim można szybko i efektywnie tworzyć wykresy, które pomagają w lepszym zrozumieniu matematycznych koncepcji. Oprogramowanie do rysowania wykresów umożliwia wprowadzenie wzorów funkcji, a następnie automatyczne generowanie wykresów, co oszczędza czas i minimalizuje ryzyko błędów. Warto zaznaczyć, że wiele z tych programów oferuje również funkcje analizy, takie jak znajdowanie miejsc zerowych czy wartości ekstremalne.
Wśród popularnych programów do rysowania funkcji znajdują się zarówno aplikacje desktopowe, jak i narzędzia online. Programy te często oferują przyjazny interfejs użytkownika oraz możliwość modyfikacji parametrów funkcji za pomocą suwaków. Użytkownicy mogą łatwo dostosować wykresy do własnych potrzeb, co czyni je idealnymi zarówno dla uczniów, jak i nauczycieli. W dalszej części artykułu przyjrzymy się konkretnym programom oraz ich funkcjom.
Przegląd popularnych programów do tworzenia wykresów
Istnieje wiele programów, które mogą pomóc w rysowaniu wykresów funkcji matematycznych. Wśród nich wyróżniają się aplikacje, które łączą funkcjonalność z łatwością obsługi. Oto kilka z nich:
- GeoGebra - wszechstronne narzędzie do nauki matematyki, które umożliwia rysowanie wykresów, a także analizę funkcji. Oferuje wiele opcji, takich jak tworzenie animacji i interaktywnych zadań.
- Desmos - intuicyjna aplikacja online, która pozwala na szybkie rysowanie wykresów funkcji. Umożliwia wprowadzanie wielu funkcji jednocześnie oraz ich modyfikację w czasie rzeczywistym.
- Graphmatica - prosty w użyciu program, który umożliwia rysowanie wykresów funkcji matematycznych oraz ich modyfikację. Dobrze sprawdza się w edukacji i analizie danych.
- Wolfram Alpha - narzędzie online, które nie tylko rysuje wykresy, ale także oblicza różne właściwości funkcji, takie jak pochodne czy całki.
- Microsoft Excel - popularne oprogramowanie, które pozwala na tworzenie wykresów na podstawie danych. Umożliwia wizualizację funkcji w formie wykresów liniowych, słupkowych i innych typów.
Jak korzystać z narzędzi online do rysowania funkcji
Narzędzia online do rysowania funkcji matematycznych oferują wygodny sposób na tworzenie wykresów bez potrzeby instalacji oprogramowania. Dzięki prostemu interfejsowi użytkownika można szybko wprowadzać wzory funkcji i natychmiastowo zobaczyć ich wykres. Takie narzędzia są idealne dla uczniów, nauczycieli oraz wszystkich, którzy chcą wizualizować matematyczne zależności. Wiele z tych aplikacji pozwala także na modyfikację parametrów funkcji, co umożliwia eksperymentowanie i lepsze zrozumienie, jak zmiany w równaniach wpływają na kształt wykresu.
Przykłady popularnych narzędzi online to Desmos, które umożliwia łatwe rysowanie wykresów oraz GeoGebra, które oferuje zaawansowane funkcje matematyczne. Użytkownicy mogą korzystać z tych narzędzi na różnych urządzeniach, co czyni je bardzo dostępnymi. Warto również zwrócić uwagę na możliwość współpracy z innymi użytkownikami, co sprzyja nauce i wymianie doświadczeń.
Jak wykorzystać rysowanie funkcji w praktycznych zastosowaniach
Rysowanie funkcji matematycznych to nie tylko akademicka umiejętność, ale także praktyczne narzędzie, które można zastosować w różnych dziedzinach. Na przykład, inżynierowie i architekci często wykorzystują wykresy funkcji do modelowania i analizy rozkładów obciążeń w konstrukcjach. Dzięki wizualizacji funkcji można lepiej zrozumieć, jak różne czynniki wpływają na stabilność budynków czy mostów. W kontekście nauk przyrodniczych, rysowanie funkcji jest kluczowe w analizie danych, gdzie wizualizacja trendów może pomóc w przewidywaniu przyszłych zjawisk, takich jak zmiany klimatyczne czy wzrost populacji.
W miarę jak technologia się rozwija, coraz więcej narzędzi online oferuje zaawansowane funkcje, takie jak symulacje i interaktywne wykresy, które pozwalają użytkownikom na eksperymentowanie z różnymi scenariuszami. To otwiera nowe możliwości w edukacji i badaniach, umożliwiając studentom i badaczom lepsze zrozumienie skomplikowanych koncepcji matematycznych oraz ich zastosowań w rzeczywistych problemach. Warto zainwestować czas w naukę tych narzędzi, aby w pełni wykorzystać ich potencjał w praktyce.

