Aby narysować parabolę, czyli wykres funkcji kwadratowej, należy wykonać kilka kluczowych kroków. Proces ten zaczyna się od zrozumienia, jak współczynnik $a$ w równaniu $y = ax^2 + bx + c$ wpływa na kierunek ramion paraboli. Gdy $a$ jest większe od zera, ramiona skierowane są do góry, a gdy jest mniejsze, do dołu. Kolejnym krokiem jest zaznaczenie punktu przecięcia paraboli z osią $Oy$, który odpowiada wartości $c$. To podstawowe informacje, które pomogą w dalszym rysowaniu wykresu.
W dalszej części artykułu przedstawimy szczegółowe metody rysowania parabol, uwzględniając różne techniki oraz przykłady, które pomogą w lepszym zrozumieniu tego zagadnienia. Niezależnie od tego, czy jesteś uczniem, studentem, czy po prostu osobą zainteresowaną matematyką, nasze wskazówki będą nieocenione w Twoich próbach rysowania parabol.
Kluczowe informacje:- Współczynnik $a$ decyduje o kierunku ramion paraboli.
- Punkt przecięcia z osią $Oy$ to $(0, c)$, gdzie $c$ to wartość w równaniu.
- Miejsca zerowe funkcji oblicza się, rozwiązując równanie kwadratowe $ax^2 + bx + c = 0$.
- Delta ($\Delta = b^2 - 4ac$) określa liczbę miejsc zerowych: dwa, jedno lub brak.
- Wierzchołek paraboli wyznacza się według wzorów $p = \frac{-b}{2a}$ i $q = \frac{-\Delta}{4a}$.
- Dokładność rysunku zwiększa się przez dodawanie dodatkowych punktów na wykresie.
Jak skutecznie narysować parabolę w kilku prostych krokach
Aby narysować parabolę, czyli wykres funkcji kwadratowej, należy wykonać kilka kluczowych kroków. Zrozumienie podstawowych właściwości parabol jest niezbędne, ponieważ pozwala na prawidłowe przedstawienie wykresu. Kluczowym elementem jest określenie kierunku ramion paraboli, który zależy od wartości współczynnika $a$ w równaniu $y = ax^2 + bx + c$. Gdy $a$ jest większe od zera, ramiona będą skierowane do góry, a gdy jest mniejsze, do dołu. Takie informacje są fundamentem dla dalszych kroków w rysowaniu paraboli.
Po określeniu kierunku ramion, należy zaznaczyć punkt przecięcia paraboli z osią $Oy$, który ma współrzędne $(0, c)$. Następnie kluczowym krokiem jest obliczenie miejsc zerowych funkcji, co można zrobić, rozwiązując równanie kwadratowe $ax^2 + bx + c = 0$. Wartość delty ($\Delta = b^2 - 4ac$) pozwala określić liczbę miejsc zerowych: gdy $\Delta > 0$, są dwa miejsca zerowe; gdy $\Delta = 0$, jedno miejsce zerowe; a gdy $\Delta < 0$, brak miejsc zerowych. Te punkty są istotne dla dokładnego narysowania wykresu.
Zrozumienie podstawowych właściwości parabol i ich równań
Parabola to krzywa, która ma wiele interesujących właściwości. W standardowej postaci, równanie parabol ma formę $y = ax^2 + bx + c$. Współczynnik $a$ określa, czy parabola jest otwarta ku górze, czy ku dołowi. Ponadto, parabola jest symetryczna względem prostej, która przechodzi przez jej wierzchołek. Wierzchołek paraboli, oznaczany jako $W$, można obliczyć za pomocą wzorów $p = \frac{-b}{2a}$ oraz $q = \frac{-\Delta}{4a}$. Zrozumienie tych właściwości jest kluczowe dla prawidłowego rysowania wykresu.
Krok po kroku: Rysowanie parabol w układzie współrzędnych
Aby narysować parabolę w układzie współrzędnych, należy zacząć od przygotowania odpowiednich narzędzi. Do rysowania będziesz potrzebować papieru milimetrowego, linijki oraz ołówka. Przygotowanie tych narzędzi ułatwi dokładne przedstawienie wykresu. Następnie, zacznij od zaznaczenia punktu przecięcia z osią $Oy$ oraz miejsc zerowych, które obliczyłeś wcześniej. Każdy z tych punktów będzie kluczowy dla dalszych działań.
Następnie, oblicz współrzędne wierzchołka paraboli. Zaznacz ten punkt na wykresie, a następnie narysuj prostą symetrii, która przechodzi przez wierzchołek. To pomoże w zachowaniu proporcji podczas rysowania krzywej. Im więcej punktów zaznaczysz, tym dokładniejszy będzie rysunek. Możesz obliczyć dodatkowe punkty, podstawiając różne wartości $x$ do równania funkcji i obliczając odpowiadające im wartości $y$.
Na końcu, po zaznaczeniu wszystkich istotnych punktów, połącz je gładką krzywą, która będzie przedstawiać parabolę. Pamiętaj, aby dostosować kształt krzywej do kierunku ramion, które wcześniej określiłeś. W ten sposób stworzysz dokładny wykres paraboli, który będzie odzwierciedlał funkcję kwadratową.
- Papier milimetrowy do precyzyjnego rysowania.
- Linijka do zachowania prostych linii i symetrii.
- Ołówek, aby móc wprowadzać korekty w trakcie rysowania.
Wykorzystanie różnych metod rysowania parabol dla lepszego zrozumienia
Rysowanie parabol to proces, który można zrealizować na wiele sposobów. Każda z metod ma swoje zalety, a ich zastosowanie zależy od poziomu zaawansowania oraz celów rysowania. Wykorzystanie różnych podejść do rysowania parabol pozwala lepiej zrozumieć, jak funkcje kwadratowe działają i jak są reprezentowane graficznie. W tym kontekście istotne jest, aby poznać zarówno metody oparte na punktach charakterystycznych, jak i te, które wykorzystują równania kwadratowe.
Wybór metody rysowania parabol może znacznie wpłynąć na dokładność i jakość wykresu. Na przykład, rysowanie za pomocą punktów charakterystycznych pozwala na łatwe zrozumienie symetrii paraboli, podczas gdy użycie równań kwadratowych umożliwia precyzyjne obliczenie wartości punktów na wykresie. Obie metody są nie tylko praktyczne, ale także edukacyjne, ponieważ pomagają w lepszym zrozumieniu matematycznych podstaw, które leżą u podstaw funkcji kwadratowych.
Rysowanie parabol za pomocą punktów charakterystycznych
Jedną z najprostszych metod rysowania parabol jest wykorzystanie punktów charakterystycznych, takich jak wierzchołek, miejsca zerowe oraz punkt przecięcia z osią $Oy$. Wierzchołek paraboli, oznaczany jako $W$, jest kluczowym punktem, w którym funkcja osiąga wartość maksymalną lub minimalną. Aby go znaleźć, należy obliczyć współrzędne wierzchołka, co można zrobić za pomocą wzorów $p = \frac{-b}{2a}$ oraz $q = \frac{-\Delta}{4a}$. Zrozumienie roli wierzchołka jest niezbędne do prawidłowego przedstawienia parabol w układzie współrzędnych.
Kolejnym ważnym punktem jest tzw. punkt przecięcia z osią $Oy$, który zawsze znajduje się w miejscu, gdzie $x = 0$. Oznacza to, że jego współrzędne to $(0, c)$, gdzie $c$ to wartość w równaniu funkcji kwadratowej. Miejsca zerowe, które można obliczyć z równania kwadratowego, również są kluczowe, ponieważ określają, gdzie parabola przecina oś $Ox$. Rysując parabolę, zaznaczając te punkty, można uzyskać dokładny kształt wykresu.
Użycie równań kwadratowych do rysowania parabol
Inną skuteczną metodą rysowania parabol jest wykorzystanie równań kwadratowych. Równanie kwadratowe ma postać $y = ax^2 + bx + c$, gdzie współczynniki $a$, $b$ i $c$ mają kluczowe znaczenie dla kształtu wykresu. Aby narysować parabolę, można obliczyć wartości $y$ dla różnych wartości $x$, co pozwala na uzyskanie punktów, które następnie można połączyć w krzywą. Ta metoda daje większą kontrolę nad dokładnością wykresu.
Warto zauważyć, że zmiana wartości współczynnika $a$ wpływa na otwarcie paraboli. Gdy $a > 0$, parabola otwiera się ku górze, a gdy $a < 0$, ku dołowi. Dzięki temu można łatwo dostrzec, jak różne równania kwadratowe wpływają na kształt paraboli. Poniższa tabela przedstawia przykłady różnych równań kwadratowych oraz odpowiadające im kształty parabol:
| Równanie | Kształt paraboli |
| $y = x^2$ | Otwarta ku górze |
| $y = -x^2$ | Otwarta ku dołowi |
| $y = 2x^2 + 3$ | Otwarta ku górze, przesunięta w górę |
| $y = -0.5x^2 - 2$ | Otwarta ku dołowi, przesunięta w dół |
Czytaj więcej: Jak narysować misia uszatka - prosty sposób na udany rysunek
Przykłady różnych parabol: Jak różne współczynniki wpływają na kształt?
Współczynniki w równaniach kwadratowych mają kluczowy wpływ na kształt oraz położenie parabol. Gdy współczynnik $a$ jest dodatni, parabola otwiera się ku górze, co oznacza, że jej wierzchołek jest najniższym punktem wykresu. Z kolei, gdy $a$ jest ujemny, parabola otwiera się ku dołowi, a wierzchołek staje się najwyższym punktem. Zmiany wartości współczynnika $b$ oraz $c$ również wpływają na położenie paraboli w układzie współrzędnych, zmieniając jej przesunięcia w poziomie i w pionie.
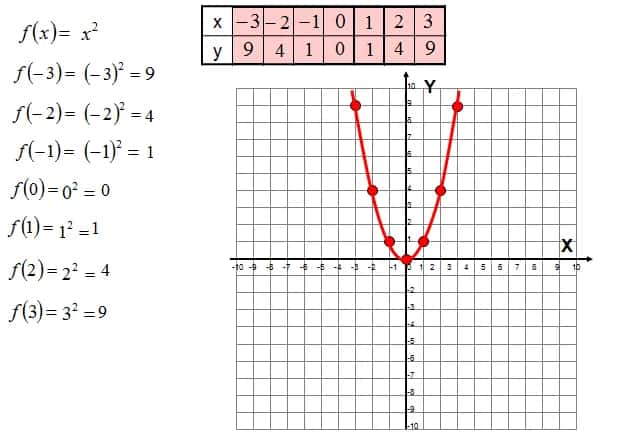
Na przykład, dla równania $y = x^2$, parabola otwiera się ku górze i ma wierzchołek w punkcie $(0, 0)$. Zmieniając równanie na $y = 2x^2$, widzimy, że parabola staje się węższa, ponieważ wartość $a$ jest większa. Z drugiej strony, równanie $y = -x^2$ ilustruje parabolę otwartą ku dołowi, co pokazuje, jak zmiana znaku współczynnika $a$ wpływa na kierunek ramion. Takie różnice są niezwykle ważne dla właściwego zrozumienia, jak różne współczynniki wpływają na kształt parabol.
Analiza parabol z dodatnimi współczynnikami
Parabole z dodatnimi współczynnikami mają charakterystyczne cechy, które można łatwo zaobserwować. Na przykład, w równaniu $y = 3x^2 + 2$, parabola otwiera się ku górze, a jej wierzchołek znajduje się w punkcie $(0, 2)$. Dzięki większej wartości współczynnika $a$, parabola jest węższa w porównaniu do równania $y = x^2$. Innym przykładem jest równanie $y = 0.5x^2 - 1$, które również otwiera się ku górze, ale jest szersze, a wierzchołek znajduje się w punkcie $(0, -1)$. Te różnice w kształcie i położeniu są kluczowe dla analizy parabol z dodatnimi współczynnikami.
- $y = x^2$: Parabola otwiera się ku górze, wierzchołek w $(0, 0)$
- $y = 3x^2 + 2$: Węższa parabola, wierzchołek w $(0, 2)$
- $y = 0.5x^2 - 1$: Szersza parabola, wierzchołek w $(0, -1)$
Analiza parabol z ujemnymi współczynnikami
Parabole z ujemnymi współczynnikami mają swoje unikalne cechy, które wpływają na ich kształt. Na przykład, równanie $y = -2x^2$ ilustruje parabolę otwartą ku dołowi, z wierzchołkiem w punkcie $(0, 0)$. Wartość współczynnika $a$ sprawia, że parabola jest węższa w porównaniu do równania $y = -x^2$. Zmieniając równanie na $y = -0.5x^2 + 1$, otrzymujemy szerszą parabolę, której wierzchołek znajduje się w punkcie $(0, 1)$. Te różnice pokazują, jak współczynniki wpływają na kształt parabol z ujemnymi wartościami.
- $y = -x^2$: Parabola otwarta ku dołowi, wierzchołek w $(0, 0)$
- $y = -2x^2$: Węższa parabola, wierzchołek w $(0, 0)$
- $y = -0.5x^2 + 1$: Szersza parabola, wierzchołek w $(0, 1)$
Wskazówki i triki na poprawne rysowanie parabol
Aby skutecznie narysować parabolę, warto znać kilka praktycznych wskazówek, które pomogą w uzyskaniu dokładnego wykresu. Po pierwsze, zawsze zaczynaj od zaznaczenia kluczowych punktów, takich jak wierzchołek, miejsca zerowe oraz punkt przecięcia z osią $Oy$. To pozwoli na lepsze zrozumienie kształtu paraboli. Po drugie, nie zapomnij o symetrii – parabola jest symetryczna względem prostej przechodzącej przez wierzchołek, co ułatwia rysowanie. Unikaj też rysowania zbyt wielu punktów, które mogą wprowadzić zamieszanie; zamiast tego skup się na kluczowych punktach.
Kolejną ważną wskazówką jest użycie odpowiednich narzędzi, takich jak papier milimetrowy i linijka, które pomogą w precyzyjnym rysowaniu. Nie należy się spieszyć – staranność w każdym kroku rysowania wpłynie na jakość końcowego wykresu. Pamiętaj również, aby regularnie sprawdzać, czy wszystkie punkty są poprawnie zaznaczone i czy krzywa jest gładka. Dzięki tym wskazówkom unikniesz najczęstszych błędów i stworzysz dokładny wykres paraboli.
Jak unikać najczęstszych błędów przy rysowaniu parabol
Podczas rysowania parabol, wiele osób popełnia typowe błędy, które można łatwo uniknąć. Przykładem jest niewłaściwe zaznaczanie punktów, co prowadzi do zniekształcenia kształtu wykresu. Innym powszechnym błędem jest pomijanie wierzchołka paraboli, co skutkuje brakiem symetrii. Warto także unikać zbyt dużej liczby punktów, które mogą wprowadzać niepotrzebne zamieszanie. Regularne sprawdzanie, czy wszystkie punkty są zaznaczone poprawnie, oraz zachowanie ostrożności podczas rysowania krzywej pomoże w uzyskaniu precyzyjnego wykresu.
Narzędzia i materiały pomocne w rysowaniu parabol
Aby narysować parabolę w sposób dokładny i estetyczny, warto zaopatrzyć się w odpowiednie narzędzia. Kluczowym elementem jest papier milimetrowy, który ułatwia precyzyjne zaznaczanie punktów. Linijka jest niezbędna do rysowania prostych linii, a ołówek pozwala na wprowadzenie korekt. Warto także mieć pod ręką gumkę do mazania, aby móc poprawić ewentualne błędy. Dobrej jakości cyrkiel może być pomocny przy rysowaniu okręgów, które są czasami używane w analizie parabol. Używając tych narzędzi, można znacznie ułatwić sobie proces rysowania parabol.
- Papier milimetrowy – idealny do precyzyjnego rysowania wykresów.
- Linijka – niezbędna do zachowania prostych linii i symetrii.
- Ołówek – pozwala na wprowadzanie poprawek i dokładne zaznaczanie punktów.
- Gumka do mazania – pomocna w usuwaniu błędów.
- Cyrkiel – przydatny do rysowania okręgów i innych kształtów pomocniczych.
Zastosowanie parabol w praktyce: Gdzie je spotykamy?
Parabole znajdują szerokie zastosowanie w różnych dziedzinach, w tym w architekturze i fizyce. W architekturze, parabola jest często wykorzystywana do projektowania struktur, które muszą wytrzymać duże obciążenia, jak na przykład mosty. Kształt paraboliczny pozwala na równomierne rozłożenie sił, co czyni te konstrukcje nie tylko estetycznymi, ale również funkcjonalnymi. W fizyce, parabolę spotykamy w kontekście ruchu ciał, szczególnie w przypadku projektów ruchu, gdzie trajektoria obiektu przyjmuje kształt paraboliczny.
W architekturze, przykłady zastosowania parabol obejmują takie budowle jak most Golden Gate w San Francisco, którego kształt jest inspirowany parabolą, oraz pawilon paraboliczny w Centrum Nauki w Doncaster. Te struktury nie tylko zachwycają swoim wyglądem, ale również są doskonałymi przykładami zastosowania matematyki w praktyce. W fizyce, parabolę możemy zaobserwować podczas rzutu ukośnego, gdzie trajektoria piłki do koszykówki tworzy kształt paraboliczny, co jest kluczowe dla zrozumienia dynamiki ruchu.
Przykłady parabol w architekturze i inżynierii
W architekturze, parabole są wykorzystywane w wielu znanych budowlach. Na przykład, most Księcia Walii w Londynie, zaprojektowany przez inżyniera Roberta Maillarta, ma paraboliczny kształt przęsła, co pozwala na efektywne przenoszenie obciążeń. Innym przykładem jest budynek Sydney Opera House, którego dachy mają kształt paraboliczny, co nie tylko nadaje mu charakterystyczny wygląd, ale również wpływa na akustykę wewnętrzną. Te przykłady pokazują, jak parabola może być używana do osiągania zarówno estetyki, jak i funkcjonalności w architekturze.
- Most Księcia Walii w Londynie – paraboliczne przęsło dla efektywnego przenoszenia obciążeń.
- Sydney Opera House – dachy o kształcie parabolicznym, poprawiające akustykę.
- Most Golden Gate w San Francisco – inspiracja parabolą w konstrukcji mostu.
Parabola w fizyce: Zastosowanie w ruchu ciał
W fizyce, parabolę można zaobserwować w kontekście ruchu ciał, szczególnie podczas rzutu ukośnego. Przykładowo, gdy piłka jest rzucana pod kątem, jej trajektoria tworzy kształt paraboliczny. To zjawisko jest kluczowe dla zrozumienia zasad fizyki ruchu, ponieważ pozwala na przewidywanie, gdzie obiekt wyląduje. Inne przykłady to trajektorie rakiet oraz ruchy ciał niebieskich, które również mogą przyjmować kształt parabol. Te zastosowania pokazują, jak ważne jest zrozumienie parabol w kontekście fizyki i inżynierii.
- Rzut ukośny piłki – trajektoria tworzy parabolę.
- Ruch rakiet – trajektoria paraboliczna w fazie wznoszenia.
- Ruch ciał niebieskich – kształt paraboliczny w niektórych orbitach.
Nowe technologie w rysowaniu parabol: Przyszłość i innowacje
W miarę jak technologia się rozwija, pojawiają się nowe narzędzia i techniki, które mogą zrewolucjonizować sposób, w jaki rysujemy parabolę i analizujemy jej właściwości. Przykładem są aplikacje komputerowe oraz oprogramowanie CAD (Computer-Aided Design), które umożliwiają inżynierom i architektom precyzyjne modelowanie parabol w trójwymiarowej przestrzeni. Dzięki tym technologiom, możliwe jest nie tylko rysowanie parabol, ale także symulowanie ich zachowania w różnych warunkach, co może być niezwykle pomocne w projektowaniu budowli czy infrastruktury.Co więcej, rozwój technologii druku 3D otwiera nowe możliwości dla architektów i inżynierów. Dzięki tej technologii można tworzyć fizyczne modele parabol, co pozwala na lepsze zrozumienie ich struktury oraz funkcjonalności. Umożliwia to także testowanie różnych kształtów i materiałów w rzeczywistych warunkach, co może prowadzić do innowacyjnych rozwiązań w budownictwie. W przyszłości, integracja analizy danych z rysowaniem parabol może pomóc w tworzeniu jeszcze bardziej efektywnych i estetycznych konstrukcji, które będą odpowiadały na potrzeby zmieniającego się świata.
